All fifths tuning
| All fifths | |
|---|---|
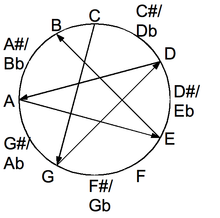 The consecutive open-notes of all-fifths tuning are each spaced seven semitones apart on the chromatic circle. | |
| Basic information | |
| Aliases | Perfect-fifths tuning |
| Interval | Perfect fifth |
| Semitones | 7 |
| Example(s) | C-G-d-a-e'-b' or G'-D-A-e-b-f♯' |
| Advanced information | |
| Other instruments | violin, cello, mandolin, tenor banjo |
| Repetition | No |
| Advantages | Wide range; natural for concert stringed-instrument music |
| Disadvantages | Difficult to play standard-guitar music |
| Left-handed tuning | All-fourths tuning |
| Associated musician | |
| Guitarist | Carl Kress |
 | |
| Carl Kress played jazz with all-fifths tuning. | |
| Regular tunings (semitones) | |
| Trivial (0) | |
| Minor thirds (3) | |
| Major thirds (4) | |
| All fourths (5) | |
| Augmented fourths (6) | |
| New standard (7, 3) | |
| All fifths (7) | |
| Minor sixths (8) | |
| Guitar tunings | |

Among guitar tunings, all-fifths tuning refers to the set of tunings in which each interval between consecutive open strings is a perfect fifth. All-fifths tuning is also called fifths, perfect fifths, or mandoguitar.[1] The conventional "standard tuning" consists of perfect fourths and a single major third between the g and b strings:
- E-A-d-g-b-e'
All-fifths tuning has the set of open strings
- C-G-d-a-e'-b' or G'-D-A-e-b-f♯',
which have intervals of 3 octaves minus a half-step between the lowest and highest string. The conventional tuning has an interval of 2 octaves between lowest and highest string.
All-fifths tuning is a tuning in intervals of perfect fifths like that of a mandolin or a violin. It has a wide range. It was used by jazz guitarist Carl Kress in the form
- B♭'-F-c-g-d'-a'.[2]
An approximation: new standard tuning
[edit]All-fifths tuning has been approximated with tunings that avoid the high b' replacing it with a g' in the New Standard Tuning of King Crimson's Robert Fripp, which has been taught in Guitar Craft courses.[3][4] Guitar Craft, which has been succeeded by Guitar Circle, has taught Fripp's tuning to 3,000 students.[5]
An approximation: through the looking glass guitar
[edit]All-fifths tuning has been approximated with tunings in the Through The Looking Glass Guitar[6] of Kei Nakano, which has been played by him since 2015. This new tuning is like a mirror to all kinds of string instruments including guitar. Also it can adapt to any other tunings of guitar. If tuned to normal guitar for the right handed person, it is able to use for lefty guitar in general, and vice versa.
An approximation: fifths with a unison pair for standard string sets
[edit]This tuning combines the wide 5th intervals with the possibility of close intervals that allows the pair of unison 3rd and 2nd strings (A). When playing in unison, this tuning also allow a chorus-like effect similar to the sound that the unison produces in 12 string guitars, but in a much smaller scale.
It was developed to be used with a standard set of strings, for example a hybrid set of 0.9 strings, and without lowering too much the range of the electric guitar. It has a range that starts from two tones lower than the standard E tuning (C2 instead of E2) for the 6st string, but the 1st string is tuned to the same note (E4). It also shares the 4th string tuning (D3) with the E standard tuning.[7]
C-G-D-A-A-E
Relation with all-fourths tuning
[edit]
All-fifths tuning is closely related to all-fourths tuning. All-fifths tuning is based on the perfect fifth (the interval with seven semitones), and all-fourths tuning is based on the perfect fourth (five semitones). The perfect-fifth and perfect-fourth intervals are inversions of one another, and the chords of all-fourth and all-fifths are paired as inverted chords. Consequently, chord charts for all-fourths tunings may be used for left-handed all-fifths tuning.[8]
See also
[edit]Notes
[edit]- ^ Sethares (2001, "The mandoguitar tuning" 62–63): Sethares, Bill (2001). "Regular tunings". Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 52–67. 2010 Alternate tuning guide, including a revised chapter on regular tunings. Retrieved 19 May 2012.
- ^ Page 92. Richard Lieberson, "Swing guitar: The acoustic chordal style", pages 89-112. The Guitar in Jazz: An Anthology, Edited by James Sallis. 1996. 978-0-8032-4250-0
- ^ Tamm, Eric (2003) [1990], Robert Fripp: From crimson king to crafty master (Progressive Ears ed.), Faber and Faber (1990), ISBN 0-571-16289-4, Zipped Microsoft Word Document, archived from the original on 26 October 2011, retrieved 25 March 2012
- ^ Zwerdling, Daniel (5 September 1998). "California Guitar Trio". All Things Considered (NPR Weekend ed.). Washington DC: National Public Radio. Retrieved 25 March 2012..
- ^ Fripp (2011, p. 3): Fripp, Robert (2011). Pozzo, Horacio (ed.). Seven Guitar Craft themes: Definitive scores for guitar ensemble. "Original transcriptions by Curt Golden", "Layout scores and tablatures: Ariel Rzezak and Theo Morresi" (First limited ed.). Partitas Music. ISMN 979-0-9016791-7-7. DGM Sku partitas001.
- ^ "日本特許第6709929号 【発明の名称】弦楽器 【特許権者】中野 圭". patents.google.com. Retrieved 2023-06-30.
- ^ CGDAAE Guitar Tuning (Fifths/Unison) - Strat in Series - Finger-picking and melodic playing demo. Retrieved 2024-05-13 – via www.youtube.com.
- ^ Sethares (2001, p. 53)
References
[edit]- Sethares, William A. (2011). "Alternate tuning guide". Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. 2010 PDF version by Bill Sethares. Retrieved 19 May 2012.
Further reading
[edit]- Denyer, Ralph (1992). "Playing the guitar: Alternative tunings". The guitar handbook. Special contributors Isaac Guillory and Alastair M. Crawford (Fully revised and updated ed.). London and Sydney: Pan Books. pp. 158–159. ISBN 0-330-32750-X.
