Talk:Function (mathematics)
| This is the talk page for discussing improvements to the Function (mathematics) article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: Index, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15Auto-archiving period: 90 days |
| This It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
| The contents of the Function (set theory) page were merged into Function (mathematics). For the contribution history and old versions of the redirected page, please see its history; for the discussion at that location, see its talk page. |
| Text and/or other creative content from this version of Function (mathematics) was copied or moved into History of the function concept with this edit. The former page's history now serves to provide attribution for that content in the latter page, and it must not be deleted as long as the latter page exists. |
| The contents of the Empty function page were merged into Function (mathematics) on 25 July 2017. For the contribution history and old versions of the redirected page, please see its history; for the discussion at that location, see its talk page. |
Function evaluation
[edit]A mini edit war has started about the paragraph on function evaluation. This paragraph was confusely written, and I rewrote it boldy for clarifiation. Nevertheless, some problems remain, for which I am not sure of the best solution.
- Although very sketchy, this paragraph is too long for the lead. I am not sure of the part of it that belong to the lead and of the best place for details.
- Function evaluation redirects here. This deserves more than two lines in the lead. Maybe a specific article?
- Very often, "function evaluation" refers more properly to "expression evaluation". The confusion between these two concepts is the cause of many errors by beginners in the use of computer algebra systems. Expression evaluation is a redirect to Expression (mathematics)#evaluation that I created recently. Nevertheless, the treatment of evaluation (mathematics) remains insufficient and confusing in Wikipedia.
- Although very common, the vertical-bar notation for evaluation is not clearly defined in Wikipedia. I added recently a description of it at Expression evaluation, but this is still insufficient. This vertical bar notation, is a particular case of a restriction, if one consider as an abbreviation of Maybe, a description of the vertical-bar notation for evaluation could be added at Restriction.
In summary, fixing this paragraph of the lead requires more work and more discussion, for which the tag {{cn}} is of no help. D.Lazard (talk) 17:39, 24 March 2024 (UTC)
- The lead section of this article seems like an inappropriate place for the only discussion of this "vertical bar notation" which is not used anywhere else in the article. It's confusing, distracting, and only tangentially relevant. It should be put somewhere else in the article or in another article. Readers aren't going to look for it here, and readers who come across it here aren't going to find it valuable in context. –jacobolus (t) 17:43, 24 March 2024 (UTC)
- One problem with this vertical bar notation is that it's hard to find clear sources describing its history/use. My guess is that it evolved out of the related notation for the bounds of a definite integral, as found in introductory calculus books/courses. There's a discussion of the earliest use (under "bar notation") in https://jeff560.tripod.com/calculus.html –jacobolus (t) 18:20, 24 March 2024 (UTC)
- The use of "often" and "commonly" are unsourced and unnecessary. The second sentence has not one, but two parenthetical clauses. Yikes! The third sentence, unnecessarily restricts itself to talk about function evaluation to the case when the expression "depends on x". This, "depends on x", is ambiguous as an intuitive notion and it hasn't been defined in the article as a formal concept. Thatwhichislearnt (talk) 13:35, 25 March 2024 (UTC)
- I agree that {{cn}} is not sufficient to elaborate on the vertical bar and evaluation, however, I consider(ed) is necessary - I apologize for my part of the "mini edit war" (I didn't intend to fight). I also agree that the vertical bar needn't be adressed in the lead, or even shouldn't be adressed there. However, it should be explained somewhere (not sure whether inside this article). And I, too, have seen the notation only in computations of definite integral [and in the recent versions of this article's lead].
- Defining the vertical bar based on restriction appears to be one possibility, which also nicely motivates the notation. Another possibility would be to define it based on substitution (logic), i.e. means the substitution application , or the evaluation of it. I'm not sure about an explanation of "expression evaluation". Maybe it should be based on (item "Functions" at) First-order_logic#Evaluation_of_truth_values, which defines evaluation of an expression in terms of evaluation of its constituent functions. (First-order logic doesn't care about how to obtain a function's result value for given inputs. If a function is defined by an expression in turn, its constituent functions (usually ) need to be evaluated, which leads to the standard arithmetical algorithms. However, a function may well be non-computable, and it may be impossible to obtain its result value. — In computer science, term rewriting systems are capable of defining every computable function. A subclass of them, the canonical term rewrite systems, guarantee that every function defined by them can be evaluated in finitely many steps to a unique normal form, i.e. a term that can't be rewritten any further; such terms are considered "values" in this setting. Arithmetical algorithms, for example, can be written as term rewriting systems that are canonical when applied to variable-free inputs, cf. "ground confluent".) - Jochen Burghardt (talk) 20:33, 25 March 2024 (UTC)
"Overriding (mathematics)" listed at Redirects for discussion
[edit]![]() The redirect Overriding (mathematics) has been listed at redirects for discussion to determine whether its use and function meets the redirect guidelines. Readers of this page are welcome to comment on this redirect at Wikipedia:Redirects for discussion/Log/2024 April 26 § Overriding (mathematics) until a consensus is reached. Tea2min (talk) 11:59, 26 April 2024 (UTC)
The redirect Overriding (mathematics) has been listed at redirects for discussion to determine whether its use and function meets the redirect guidelines. Readers of this page are welcome to comment on this redirect at Wikipedia:Redirects for discussion/Log/2024 April 26 § Overriding (mathematics) until a consensus is reached. Tea2min (talk) 11:59, 26 April 2024 (UTC)
Function is Overloaded in definition and meaning, this article should be a survey
[edit]The function as relation or mapping in the single and multiple-valued and in classical functions, continuous functions, smooth functions, and about the language of functions, and domains and ranges and images and codomains, is very overloaded. This article is picking a course of opinion which does not represent its wide and varied usage, function the term. Over time, as other aspects of mathematics solidified, it's "function" the term that is most loosely thrown about, then as with regards to relations that are admitted to various sub-fields, each claiming their own definition of function has those are each distinct and different ant not compatible. This article, which could be called "mappings" instead as that's largely what it defines, does not from the outset affect to describe the development of the definition over time, nor does it very well reflect the most usual sort of arithmetic definition with which most people are familiar, or as with regards to domain and range. Mathematics is not merely differential geometry, and the definition of function is among the very most general and general throughout. So, this article should largely start explaining that "function theory" is its own sort of world, and a history and survey of "this is what is called a function historically or in these various settings", then with regards to an opinion of "this is a function today and in the most usual setting", which it is largely arguable that this article does not reflect, instead expect.
It reminds one of "graph", "chart", and "plot", about diagrams of functions, drawing a function.
Functions are modern, and Cartesian thus including the multi-valued, and not just classical functions, smooth classical continuous functions that are single-valued, and not just differential geometry's functions with neither vertical nor horizontal tangent, "functions" in mathematics are very general, and sub-fields that restrict the definition for their own purpose are presumptious that their definition is implicit, where it is not.
This article is opinionated and needs context in itself why the definition of function is so broad that it's about its own sub-field of mathematics, in matters of relation.
This article needs a brief survey of the development of the term over time, and to point to the many different intended interpretations of the term.
This article needs a thorough introduction detailing the survey of the meaning of the term "function" over time as mathematics has grown, and, specifically not removing what has become its fuller definition, in the interest of su-fields that would restrict its meaning for their own purposes in notation, where instead they should declare their own regions of syntax, because general usage does not agree.
This article has problems and hides them. 97.113.179.80 (talk) 15:03, 19 May 2024 (UTC)
- Are you volunteering to track down a pile of sources and write that draft? –jacobolus (t) 21:01, 19 May 2024 (UTC)
- Keeping in mind the goal of simultaneously being readable to middle-schoolers and providing pointers to current research-level mathematics... —David Eppstein (talk) 21:03, 19 May 2024 (UTC)
Why Set Theory?
[edit]As noted somewhere above, the intent was to introduce something that is usable in schools mathematics courses. Ok, nice. But why not mention it explicitly? Why not say right away (I guess it was before) that this definition is specific for set theories.
Or we could add a section dedicated to the history of the term an the notion. Leibnitz, Newton, Cauchy had no clue about functions being their graphs ("pairs of values").
To me, it's a shame to promote just one specific view of things, the school-level mathematics. It's so XX century, the century were everything was "defined" as sets. These days mathematicians must be familiar with model theory, and see clearly that functions as "sets of pairs of sets" is just a model (in sets).
Vlad Patryshev (talk) 00:38, 17 June 2024 (UTC)
- I agree. The "Formal definition" section should be expanded to note that the graph definition is one possible formalization. We should concisely explain alternatives (e.g. other constructions, or an axiomatic approach) for which we can find citations. But keep in mind WP:UNDUE as the graph definition probably remains the most common or conventional one.
- In fact, the existing text under "Formal definition" should be cut down. As written, it's not terrible, but it repeats essentially the same definition twice. Invoking the concept of a relation is unnecessary to explain the concept of the graph of a function, and its verbosity only distracts. I think it would be better to state just the graph definition directly, with a concise note that "This graph can also be viewed as defining a binary relation between the domain and codomain ".
- It might also be worth connecting the graph-based definition to the "Multi-valued functions" section further down, as the graph definition is more natural for that generalization than for the basic concept of a function. 73.223.72.200 (talk) 02:25, 28 July 2024 (UTC)
- In fact, we already have an article covering the history: History of the function concept. So perhaps we only need to explain the math of a few selected alternative formalizations without regard to their history. We can then link to the history article in lieu of putting in detailed history in this overview article. 73.223.72.200 (talk) 02:38, 28 July 2024 (UTC)
- The text could be improved by removing the two conditions in the middle of the text and only using a worded definition followed by the set-builder form. Roryyarr (talk) 12:14, 28 September 2024 (UTC)
- Please, be more accurate: where the text should be modified and which conditions should be removed" D.Lazard (talk) 14:05, 28 September 2024 (UTC)
- Paragraph 3 of the formal definition subsection is redundant as paragraph 5 presents the same information. Below is a suggested edit.
- === Formal definition ===
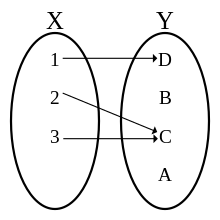
Diagram of a function 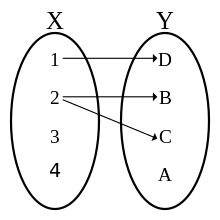
Diagram of a relation that is not a function. One reason is that 2 is the first element in more than one ordered pair. Another reason is that neither 3 nor 4 are the first element (input) of any ordered pair therein - The above definition of a function is essentially that of the founders of calculus, Leibniz, Newton and Euler. However, it cannot be formalized, since there is no mathematical definition of an "assignment". It is only at the end of the 19th century that the first formal definition of a function could be provided, in terms of set theory. This set-theoretic definition is based on the fact that a function establishes a relation between the elements of the domain and some (possibly all) elements of the codomain. Mathematically, a binary relation between two sets X and Y is a subset of the set of all ordered pairs such that and The set of all these pairs is called the Cartesian product of X and Y and denoted Thus, the above definition may be formalized as follows.
- A function is formed by three sets, the domain the codomain and the graph that satisfy the three following conditions.
- Roryyarr (talk) 11:07, 29 September 2024 (UTC)
- I have edited the article for clarifying that the definitions are the same. However the two versions must been kept, because most people do not like to read a big succession of formulas without prose, while other prefer to not refer to relation theory or need help for formalizing prose. D.Lazard (talk) 11:44, 29 September 2024 (UTC)
- Thank you D.Lazard Roryyarr (talk) 14:09, 29 September 2024 (UTC)
- I have edited the article for clarifying that the definitions are the same. However the two versions must been kept, because most people do not like to read a big succession of formulas without prose, while other prefer to not refer to relation theory or need help for formalizing prose. D.Lazard (talk) 11:44, 29 September 2024 (UTC)
- Please, be more accurate: where the text should be modified and which conditions should be removed" D.Lazard (talk) 14:05, 28 September 2024 (UTC)




















