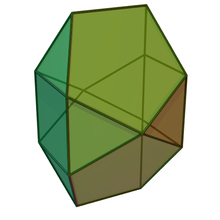
Bilunabirotunda
| Bilunabirotunda | |
|---|---|
 | |
| Type | Johnson J90 – J91 – J92 |
| Faces | 8 triangles 2 squares 4 pentagons |
| Edges | 26 |
| Vertices | 14 |
| Vertex configuration | 4(3.52) 8(3.4.3.5) 2(3.5.3.5) |
| Symmetry group | |
| Properties | convex, elementary |
| Net | |
 | |

In geometry, the bilunabirotunda is a Johnson solid with faces of 8 equilateral triangles, 2 squares, and 4 regular pentagons.
Properties
[edit]The bilunabirotunda is named from the prefix lune, meaning a figure featuring two triangles adjacent to opposite sides of a square. Therefore, the faces of a bilunabirotunda possess 8 equilateral triangles, 2 squares, and 4 regular pentagons as it faces.[1] It is one of the Johnson solids—a convex polyhedron in which all of the faces are regular polygon—enumerated as 91st Johnson solid .[2] It is known as the elementary polyhedron, meaning that it cannot be separated by a plane into two small regular-faced polyhedra.[3]
The surface area of a bilunabirotunda with edge length is:[1] and the volume of a bilunabirotunda is:[1]
Cartesian coordinates
[edit]One way to construct a bilunabirotunda with edge length is by union of the orbits of the coordinates under the group's action (of order 8) generated by reflections about coordinate planes.[4]
Applications
[edit]Reynolds (2004) discusses the bilunabirotunda as a shape that could be used in architecture.[5]
Related polyhedra and honeycombs
[edit]Six bilunabirotundae can be augmented around a cube with pyritohedral symmetry. B. M. Stewart labeled this six-bilunabirotunda model as 6J91(P4).[6] Such clusters combine with regular dodecahedra to form a space-filling honeycomb.

|
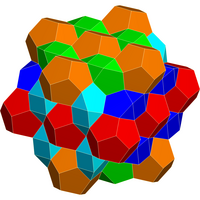 Spacefilling honeycomb |
 6 bilunabirotundae around a cube |
12 bilunabirotundae around a dodecahedron |
References
[edit]- ^ a b c Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
- ^ Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 86–87, 89. ISBN 978-0-521-66405-9.
- ^ Timofeenko, A. V. (2009). "The Non-Platonic and Non-Archimedean Noncomposite Polyhedra". Journal of Mathematical Sciences. 162 (5): 710–729. doi:10.1007/s10958-009-9655-0.
- ^ Reynolds, M. A. (2004). "The Bilunabirotunda". Nexus Network Journal. 6: 43–47. doi:10.1007/s00004-004-0005-8.
- ^ B. M. Stewart, Adventures Among the Toroids: A Study of Quasi-Convex, Aplanar, Tunneled Orientable Polyhedra of Positive Genus Having Regular Faces With Disjoint Interiors (1980) ISBN 978-0686119364, (page 127, 2nd ed.) polyhedron 6J91(P4).







