Lunar precession

Lunar standstill: every 18.6 years, the declination range of the Moon reaches a maximum or minimum.

Lunar precession is a term used for three different precession motions related to the Moon. First, it can refer to change in orientation of the lunar rotational axis with respect to a reference plane, following the normal rules of precession followed by spinning objects. In addition, the orbit of the Moon undergoes two important types of precessional motion: apsidal and nodal.

Axial precession

Main article: Axial precession

The rotational axis of the Moon also undergoes precession. Since the Moon's axial tilt is only 1.5° with respect to the ecliptic (the plane of Earth's orbit around the Sun), this effect is small. Once every 18.6 years, the lunar north pole describes a small circle around a point in the constellation Draco, while correspondingly, the lunar south pole describes a small circle around a point in the constellation Dorado. Similar to Earth, the Moon's axial precession is westwards - whereas Apsidal precession is in the same direction as the rotation (meaning apsidal precession is eastward).

Apsidal precession

Main article: Apsidal precession

Apsidal precession occurs when the direction of the major axis of the Moon's elliptic orbit rotates once every 8.85 years in the same direction as the Moon's rotation itself. This image looks upwards depicting Earth's geographic south pole and the elliptical shape of the Moon's orbit (which is vastly exaggerated from its almost circular shape to make the precession evident) is rotating from white to greyer orbits.

Animation of Moon orbit around Earth
  Moon ·   Earth
Top: Polar view; Bottom: Equatorial view

This kind of precession is that of the major axis of the Moon's elliptic orbit (the line of the apsides from perigee to apogee), which precesses eastward by 360° in approximately 8.85 years. This is the reason that an anomalistic month (the period the Moon moves from the perigee to the apogee and to the perigee again) is longer than the sidereal month (the period the Moon takes to complete one orbit with respect to the fixed stars). This apsidal precession completes one rotation in the same time as the number of sidereal months exceeds the number of anomalistic months by exactly one, after about 3,233 days (8.85 years).

Nodal precession

Approximate axial parallelism of the Moon's orbit results in relative revolution of the lunar nodes as the Earth revolves around the Sun. This causes an eclipse season approximately every six months. Nodal precession occurs every 18.6 years.

The lunar nodes are the points where the Moon's orbit intersects the ecliptic.

Main article: Nodal precession

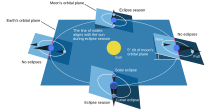
Another type of lunar orbit precession is that of the plane of the Moon's orbit. The period of the lunar nodal precession is defined as the time it takes the ascending node to move through 360° relative to the vernal equinox (autumnal equinox in the Southern Hemisphere). It is about 18.6 years and the direction of motion is westward, i.e., in the direction opposite to the Earth's orbit around the Sun. This is the reason that a draconic month or nodal period (the period the Moon takes to return to the same node in its orbit) is shorter than the sidereal month. After one nodal precession period, the number of draconic months exceeds the number of sidereal months by exactly one. This period is about 6,793 days (18.60 years).

As a result of this nodal precession, the time for the Sun to return to the same lunar node, the eclipse year, is about 18.6377 days shorter than a sidereal year. The number of solar orbits (years) during one lunar nodal precession period equals the period of orbit (one year) divided by this difference, minus one: ⁠365.2422/18.6377⁠ − 1.

The precession cycle affects the heights of tides. During half the cycle, the high and low tides are less extreme; in the other half of the cycle, they are amplified, with high tides greater than average and low tides lower than average.

See also

• Lunar theory
• Orbit of the Moon

References

• Seidelmann, P.K., ed. (1992). Explanatory Supplement to the Astronomical Almanac. U.S. Naval Observatory / University Science Books. pp. 114–115, 701.